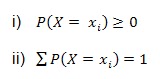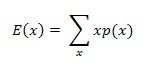VARIABLE ALEATORIA
Definición: Una variable aleatoria (v.a.) es una función que asigna un numero real a cada resultado de un espacio muestra.
Se acostumbra representarlas por lo general con las letras mayúsculas X,Y,Z y los posibles valores que pueden tomar por las letras minúsculas x,y,z, en este estudio utilizaremos la X mayúscula y la x minúscula respectivamente.
“Las variables aleatorias pueden ser discretas o continuas”.
VARIABLE ALEATORIA CONTINUA
Una variable continua tiene la propiedad de que entre 2 cualesquiera valores observables (potencialmente), hay otro valor observable (potencialmente). Una variable continua toma valores a lo largo de un continuo, esto es, en todo un intervalo de valores. Longitudes y pesos son ejemplos de variables continuas. La estatura de una persona, pude ser 1.70 mts. ó 1.75 mts., pero en potencia al menos podría tomar cualquier valor intermedio como 1.73 mts. por ejemplo.
Un atributo esencial de una variable continua es que, a diferencia de lo que ocurre con una variable discreta, nunca se la puede medir exactamente. Con una variable continua debe haber inevitablemente un error de medida.
Un importante principio sobre variables continuas es que siempre se registran en forma discreta, quedando la magnitud de la distancia entre valores registrables adyacentes determinada por la precisión de la medición.
VARIABLE ALEATORIA DISCRETA
Definición: Las variables aleatorias discretas son aquellas que solamente pueden tomar un número finito o infinito contable de valores (NUMEROS ENTEROS).
DISTRIBUCION DE PROBABILIDAD
Definición: En general llamaremos distribución de probabilidad o función de probabilidad a una tabla o formula que asocie con cada valor de una variable aleatoria su probabilidad respectiva.
X=xi | x1 | x2 | x3 | ..................... | xn |
P(X=xi) | P(X1) | P(X2) | P(X3) | ..................... | P(Xn) |
Donde:
FUNCION DE DISTRIBUCION ACUMULADA
Si X es una variable aleatoria con función de probabilidad f(X), entonces F(X), es la función escalonada definida por:
F(X) determina en forma única la distribución de probabilidad acumulada de la variable aleatoria asociada.
VALOR ESPERADO (Media, Esperanza,Ganancia esperada)
La esperanza matemática de una variable aleatoria discreta X, con una función de probabilidad p(x) y h(x) se define como:
Si h(x) = x, la esperanza o valor esperado de la variable aleatoria X, con función de probabilidad P(x), se representa por E(x) y esta dada por:
La esperanza de x es conocida como la media poblacional si, p(x) representa la distribución de frecuencias de la población. Denotarse como:
Ganancia Esperada
En un juego de azar es calculada con la esperanza matematica y se obtiene multiplicando la cantidad que el jugador espera ganar por la probabilidad de que la gane. Para que un juego sea justo la ganancia esperada debe ser cero, esto significa que un jugador en promedio termina sin ganancia ni perdida.
Cuando hablamos de perdida se habla de cantidades negativas y al hablar de ganancia de numeros positivos.
VARIANZA Y DESVIACIÓN ESTÁNDAR
Sea X una variable aleatoria discreta. Se define la varianza o variancia representada por V(x) 0 Ƃ2 con función de probabilidad P(x) por:
DESVIACION ESTANDAR
Se define como desviación estándar como:
Se define como desviación estándar como:
Ejemplos:
Ejemplo 1
En un local que vende accesorios para computadoras, cuentan con 9 computadoras ensambladas, 5 de ellas no están completas. Un cliente de un ciber-cafe adquiere 4 de estas computadoras. Un empleado nuevo elije estas maquinas aleatoriamente de entre las 9 disponibles, sea X el numero de computadoras completas con que cuenta este local. Encuentra la función de probabilidad, la función de distribución acumulada, la media, la varianza y su desviación estándar.
x= # de computadoras completas x= 0, 1, 2, 3, 4 IDENTIFICAMOS X Y SUS VALORES
r= 4
REALIZAMOS LAS OPERACIONES PARA SACAR LA PROBABILIDAD PARA CADA VALOR DE X:
PASAMOS LOS VALORES A LA TABLA
Función de probabilidad
x | 0 | 1 | 2 | 3 | 4 |
P(x) | 0.0397 | 0.3175 | 0.4762 | 0.1587 | 0.0079 |
SUMAMOS LOS VALORES DE LAS PROBABILIDADES HASTA OBTENER 1
Función de distribución acumulada
x | P(x) | F(x) |
0 | 0.0307 | 0 + 0.0397 = 0.0397 |
1 | 0.3175 | 0.0397 + 0.3175 = 0.3572 |
2 | 0.4762 | 0.3572 + 0.4762 = 0.8334 |
3 | 0.1587 | 0.8334 + 0.1587 = 0.9921 |
4 | 0.0079 | 0.9921 + 0.0079 = 1 |
.bmp)
OBTENEMOS LA MEDIA :
Media
M= (0 * 0.0397) + (1 * 0.3175) + (2 * 0.4762) + (3 * 0.1587) + (4 * 0.0079) = 1.7776
OBTENEMOS LA VARIANZA:
Varianza
V(x) = ((0 - 1.7776)2 * 0.0397) + ((1 – 1.7776)2 * 0.3175) + ((2 – 1.7776)2 * 0.4762) +
((3 – 1.7776)2 * 0.1587) + ((4-1.7776)2 * 0.0079) = 0.6169
OBTENEMOS LA DESVIACION ESTANDAR:
Desviación Estándar
Ƃ = √0.6169 = 0.785
Ejemplo 2
Un apostador en el hipodromo de las americas puede lograr una ganancia en cada carrera de $40 o una perdida de $10 por boleto, las probabilidades de que esto ocurra son de 0.60 y 0.40. Calcula la ganancia esperada.
x | -10 | 40 |
P(x) | 0.40 | 0.60 |
La esperanza es: E(x)= (-10)(0.40)+(40)(0.60)= -4+24=$20